Polinomio irreducible — Saltar a navegación, búsqueda En Teoría de Anillos, un polinomio no constante (y por lo tanto no nulo) p con coeficientes en un dominio íntegro R (es decir, ) es irreducible si no puede factorizarse como producto de polinomios de manera que todos … Wikipedia Español
Polinomio primitivo — Saltar a navegación, búsqueda Un polinomio primitivo puede referirse a uno de los dos siguientes conceptos: Un polinomio sobre un dominio de factorización única (como el de los enteros) tal que el máximo común divisor de sus coeficientes es 1. El … Wikipedia Español
Polinomio separable — Saltar a navegación, búsqueda En matemática, un polinomio P(X) es separable sobre un cuerpo K si sus raíces en una clausura algebraica de K son distintas es decir P(X) tiene factores lineales distintos en una extensión de cuerpo suficientemente… … Wikipedia Español
Polinomio todo en uno — Saltar a navegación, búsqueda Un polinomio todo en uno (AOP, All in One Polynom) es un polinomio usado en campo finitos, especificalmente GF(2) (binario). El AOP es un 1 polinomio igualmente espaciado. Un AOP de grado m tiene todos los términos… … Wikipedia Español
Polinomio mínimo — Saltar a navegación, búsqueda En matemática, el polinomio mínimo de un elemento α es el polinomio mónico p de menor grado tal que p(α)=0. Las propiedades del polinomio mínimo dependen de la estructura algebraica a la cual pertenece α. Teoría de… … Wikipedia Español
Elemento algebraico — Saltar a navegación, búsqueda Un elemento algebraico sobre un cierto cuerpo matemático es un elmento de un conjunto que contiene a dicho cuerpo matemático y que constructible a partir de ciertas operaciones algebraicas relacionadas con los… … Wikipedia Español
Extensión de cuerpo — Saltar a navegación, búsqueda En Álgebra, las extensiones de cuerpo son el problema fundamental de la Teoría de Cuerpos. Un cuerpo es un conjunto en el que las operaciones suma y producto están definidas y funcionan bien . Cuando se construye una … Wikipedia Español
Cuerpo finito — Saltar a navegación, búsqueda En álgebra abstracta, un cuerpo finito, campo finito o campo de Galois (llamado así por Évariste Galois) es un cuerpo que contiene un número finito de elementos. Los cuerpos finitos son importantes en teoría de… … Wikipedia Español
Raíz de la unidad — Saltar a navegación, búsqueda En matemática, las raíces n ésimas de la unidad, o números de de Moivre, son todos los números complejos que resultan 1 cuando son elevados a una potencia dada n. Se puede demostrar que están localizados en el… … Wikipedia Español
Transformación de Tschirnhaus — En matemáticas , una transformación de Tschirnhaus, desarrollado por Ehrenfried Walther von Tschirnhaus en 1683, es un tipo de asignación de polinomios . Puede definirse convenientemente por medio de la teoría del campo , como la transformación… … Wikipedia Español
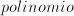 no constante (y por lo tanto no nulo)
no constante (y por lo tanto no nulo) 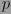 con coeficientes en un dominio íntegro
con coeficientes en un dominio íntegro 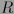 (es decir,
(es decir, 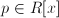 ) es irreducible si no puede factorizarse como producto de polinomios de manera que todos ellos tengan grados menor que
) es irreducible si no puede factorizarse como producto de polinomios de manera que todos ellos tengan grados menor que 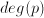 . Es decir, si
. Es decir, si 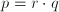 entonces ha de ser
entonces ha de ser 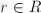 o
o 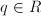 (es decir, alguno de ellos ha de ser un polinomio constante).
(es decir, alguno de ellos ha de ser un polinomio constante).